Masha Gessen’s Perfect Rigor is a fascinating biography of Grigory (Grisha) Perelman, the fearsomely brilliant and notoriously antisocial Russian mathematician. Perelman proved the Poincaré Conjecture, one of mathematics’ most important and intractable problems, in 2002—almost a century after it was first posed, and just two years after the Clay Mathematics Institute offered a one-million-dollar prize for its solution.
Gessen herself grew up in the former Soviet Union, is roughly Perelman’s age, and has a mathematical background, which facilitated her interviews with many of his classmates, mentors, teachers, and colleagues. Not surprisingly, she did not interview the reclusive mathematician or his mother, with whom he currently lives. But the others give a convincing picture not only of him but also of the strange world of Soviet mathematics, which was divided between the official, rigid mathematical establishment and the informal mathematical counterculture. The former, because of its historical importance to engineering and military projects, was supported by the Party and the government; the latter consisted of scholars who loved mathematics for its own sake and used it as a way to escape the stultifying influence of officious apparatchiks.
Born in 1966 to Jewish parents, Perelman came of age when this distinction was breaking down during the era of glasnost and perestroika. By the time he was ten he began to show a talent for mathematics, and his mother, who had abandoned her own graduate work in the field in order to raise him, enrolled him in an after-school math club coached by Sergei Rukshin, a mathematics undergraduate at Leningrad University. Rukshin was a troubled youth who became obsessed with mathematics and gradually developed a rigorous, distinctive, and very effective method of teaching problem-solving. Over the last twenty years, approximately half of all Russian entrants to the International Mathematical Olympiad have studied with him.
Only nineteen himself when he met Perelman, Rukshin stayed in contact with him from his first after-school math club until, it seems, a relatively recent break. He found that the not yet adolescent Perelman, described by Gessen as “an ugly duckling among ugly ducklings…pudgy and awkward,” was already unusually deliberate and precise in his thinking. Alexander Golovanov, who studied math alongside Perelman, said that Rukshin’s growing commitment to and love for Perelman came to give meaning to his own life. Like many a competitive sports coach, Rukshin hated it when his charges engaged in anything other than his sport. This was an unnecessary restriction in Perelman’s case since from the beginning he seemed uninterested in girls or anything other than mathematics.
When Perelman was fourteen, Rukshin spent the summer tutoring him in English; he accomplished in a few months what generally took four years of study. Perelman had to fulfill the English requirement to get into Leningrad’s Specialized Mathematics School Number 239. As Gessen writes, these mathematical high schools owe much to Andrei Kolmogorov, arguably the most important Soviet mathematician of the twentieth century and a figure who straddled the divide in Soviet mathematics mentioned above.
Kolmogorov, who did seminal work in probability, complexity theory, and other subjects, was something of an anomaly. A prolific mathematician, he was also passionately interested in education and devised an imaginative secondary school curriculum featuring mathematics first of all, but also classical music, sports, hiking, literature, poetry, and activities intended to foster male bonding. In the schools that he inspired, his disciples promoted Greek and Renaissance values and tried to protect their students from Marxist indoctrination. Eventually Kolmogorov was denounced as an agent of Western influence in the Soviet Union, but his ideas still permeated School 239 when Perelman studied there.
Valery Ryzhik, Perelman’s teacher at School 239, remembered him as “such a little boy” who sat in the back of the class. Ryzhik and Rukshin employed Kolmogorovian methods of instruction and character-building and dragooned the students into long walks, which Perelman endured but didn’t enjoy. A brilliant man himself, Ryzhik was denied entry to Leningrad University because he was Jewish, but Perelman, as he is described here, seemed oblivious not only to Ryzhik’s past difficulties, but also to the pervasive Soviet anti-Semitism and, indeed, to any sort of political issues.
The school insulated Perelman and allowed him to think that the world, like the math classroom, was a place where logic mattered and rules were interpreted strictly. It also allowed him to grow his fingernails until they curved. And if he wanted to eat only a particular kind of raisin bread with peanuts on the surface (which he didn’t like and scraped off), he could do so. Ensconced in his mathematical cocoon, he could tune out all the messy inconsistencies and contingencies of life in general and of Soviet life in particular.
Advertisement
As he approached the end of his days at School 239, Perelman had to think about the next stage of his education. Gessen writes that for a Jewish boy gifted in mathematics to be admitted to a university, there were three possibilities: hope you were one of the two Jews accepted at Leningrad University every year; go somewhere with less draconian admission policies; or make it onto the Soviet team for the International Mathematical Olympiad, which guaranteed admission to Leningrad University. Perelman decided to try out for the team.
Accompanied by his seemingly omnipresent mother, he embarked on a grueling training program held in a town near Moscow and run by Alexander Abramov, who later remarked that Perelman never encountered a problem in a competition that he couldn’t solve. He won a gold medal in the 1982 Olympiad with a perfect score and gained admission to Leningrad University.
After Abramov, Perelman’s mentors and teachers were world-class mathematicians in their own right, and Gessen provides brief sketches of all of them. In particular, there were Viktor Zalgaller, his undergraduate adviser at Leningrad University and an eminent geometer; Alexander Danilovich Alexandrov, his graduate adviser and a distinguished mathematician and philosopher; and Alexandrov’s student Yuri Burago, another prominent differential geometer. The latter two were instrumental in getting Perelman a postdoctoral position at the Steklov Institute of Mathematics in Leningrad. Mikhail Gromov was yet another important mathematician who on several occasions helped ease Perelman’s way into the larger mathematical world.
A big part of that larger world was the US, and in the late 1980s and early 1990s Perelman worked on theorems in Riemannian geometry as a postdoctoral fellow at a number of American universities, including NYU, SUNY Stony Brook, and UC Berkeley. After succinctly and elegantly proving a topological theorem called the Soul Conjecture—which dealt with the use of small parts (“souls”) of certain geometrical figures to deduce the wholes—in 1994, Perelman was widely recognized as a star and offered positions at both Stanford and Princeton. He declined both offers, rejecting Princeton’s because the math department had the temerity, in his view, to ask for a CV. Perelman thought the results he’d already proved and a lecture he’d given there should have been sufficient to warrant granting him immediate tenure. In 1995 he returned to the Steklov Institute.
The next year the European Mathematical Society planned to announce the award of a prize to Perelman, and he responded by saying he’d create an unpleasant scene if he was given it. According to Gromov, he believed that his work was not complete, that the judges were not qualified to assess it, and that he, not they, should decide when he should receive a prize.
Gessen, on the basis of many incidents of Perelman’s prickliness, his long hair and fingernails and Rasputin-like appearance, and his often asocial behavior, suggests that he has Asperger’s syndrome, sometimes referred to as autism-lite. Quoting the psychologist Simon Baron-Cohen, an expert in the field, she writes that people with Asperger’s have limited social skills, have trouble communicating, often speak oddly (their speech is characterized sometimes by jarring transitions, literal interpretations, or obliviousness to nuance), and frequently need help with the minutiae of everyday living and so are dependent on others, such as their mothers, as was the case with Perelman.
Moreover, they are extraordinarily good at systematizing but extraordinarily poor at empathizing, and have what Baron-Cohen calls an “extreme male brain.” They lack a built-in “theory of mind,” the ability both to easily imagine other people’s points of view and to realize that others will evaluate situations differently. For them, truth is literal and uniform. For example, seeing that a ball has been moved from one cup to another while someone has left the room, many people with Asperger’s expect that on the person’s return he will know that the ball is now in the other cup.
In part because of their training, mathematicians deal with universal statements and often tend to interpret assertions literally. (For a personal example, whenever I see the bumper sticker “War is never the answer,” I think that, to the contrary, war most certainly is the answer, if the question is “What is a three-letter word for organized armed conflict?”) Baron-Cohen thinks there’s more to the matter than this, however. He maintains that there is some neurological reason for the strong correlation between mathematical talent and Asperger’s syndrome. Whether true or not, mathematicians do score consistently higher on what he calls his AQ (autism-spectrum quotient) test, and Gessen writes that she herself has a high AQ. Although there are many gregarious mathematicians, there may be some truth in the definition of an extroverted one: he’s the one who looks at your feet while he’s talking.
Advertisement
Still, Perelman’s behavior, unusual as it sometimes has been, doesn’t seem all that peculiar to me. I suspect that a small part of the appeal of his story depends on the satisfaction people derive from reading about unbalanced scientists and mathematicians. Witness the popularity of A Beautiful Mind , the biography of John Nash, or The Strangest Man , the recent biography of the physicist Paul Dirac.1 The phenomenon is vaguely akin to the schadenfreude elicited by tabloids’ tales of celebrities’ faults and foibles.
Perelman seemed to fade from the mathematics scene after 1995, but then in 2002 and 2003 he posted on the Internet (rather than submit to a journal) three papers in which he sketched a proof of the Poincaré Conjecture, as well as some more general results. It is these three papers that Gessen calls “the mathematical breakthrough of the century” in the subtitle of her book. What is the Poincaré Conjecture? Useful in understanding it are a few ideas from topology, the branch of geometry concerned with the basic properties of geometric figures that remain unchanged when they are stretched and shrunk, deformed and distorted, or subjected to any “smooshing,” as long as they’re not ripped or punctured. Size and shape are not topological properties; figures shaped like melons, dice, and baseball bats are deemed topologically equivalent since they can be contracted, expanded, and transformed into one another without ripping or puncturing.

Richard Morris/Wikipedia
A diagram showing ‘simple connectedness,’ a topological property allowing for, in this example, a rubber band around the surface of a sphere to be shrunk to no more than a point. This property was long known to characterize two-dimensional spheres and has now been shown to characterize three-dimensional spheres as well by Perelman’s proof of the Poincaré Conjecture.
Whether a closed curve in space has a knot in it or not is, however, a topological property of the curve in space. That a closed non-self-intersecting curve on a flat plane, no matter how convoluted it is, divides the plane into two parts—the inside and the outside—is a topological property of the curve. How many dimensions a geometric figure possesses, whether or not it has a boundary, and if so of what sort—these too are topological properties.
Also a matter of topological significance is the genus of a figure—the number of holes it contains. A ball has genus 0 since it contains no holes; a torus (a doughnut, bagel, or inner tube–shaped figure) has genus 1; eyeglass frames without the lenses have genus 2; and so on. Genus 0 objects such as melons and baseball bats are topologically equivalent. Less obviously, a doughnut and a coffee cup with a handle are both figures of genus 1. To see this, imagine that the cup is made of clay. Flatten the body of the cup and expand the size of its handle by squeezing material from the body into the handle. The finger hole of the cup’s handle is in this way transformed into the hole of the doughnut.
Henri Poincaré was a French mathematical polymath who laid the foundation for chaos theory and came close to discovering the theory of relativity, among other accomplishments. In a 1904 paper he famously wondered whether a certain topological property of a sphere holds for higher-dimensional analogues of a sphere.
To understand that property, imagine stretching a rubber band around the surface of a ball. We can contract this rubber band slowly, making sure it neither breaks nor loses contact with the ball, and in this way shrink the rubber band so that it becomes no more than a point. (See illustration on this page.) We can’t shrink it to a point if the rubber band is stretched around a doughnut (either around the hole or around the body) or around a pretzel. We can do it, however, if the rubber band is stretched around any topological equivalent of a smooshed ball such as a deformed melon, a crooked die, or a baseball bat with protuberances sticking out of it.
The surface of the ball, but not that of the doughnut, is said to be “simply connected.” Poincaré was aware of the fact that a two-dimensional sphere—the topological term for the two-dimensional surface of a three-dimensional ball—could be defined by this property of simple connectivity. That is, any simply connected two-dimensional closed surface, however distorted, is topologically equivalent to the surface of a ball. He wondered if simple connectedness might characterize three-dimensional spheres as well. The statement that it does so is the Poincaré Conjecture.
This may not sound that daunting until we understand what a three-dimensional sphere is. Topologically speaking, a one-dimensional sphere is the boundary of a circle, i.e., a one-dimensional line of constant curvature on a two-dimensional plane. And, as mentioned, a two-dimensional sphere is the two-dimensional surface of a ball in three-dimensional space. A three-dimensional sphere would be a formally analogous but much more abstract entity: the three-dimensional boundary of a ball in four-dimensional space.
This fourth dimension is easy to define formally but difficult to grasp, except by analogy. Two numerical coordinates are needed to locate a point on a two-dimensional plane, and three to locate it in a three-dimensional space; four-dimensional space is that hypothetical space in which four coordinates are needed. It contains four-dimensional equivalents to our familiar three-dimensional geometrical objects—a four-dimensional cube, for example, known as a tesseract, that has sixteen corners and thirty-two edges to a cube’s eight and twelve. (See illustration on page 45.) A four-dimensional ball, then, would have the same relation to a normal three-dimensional ball that that three-dimensional ball has to the two-dimensional interior of a circle. Such a four-dimensional ball, and the three-dimensional sphere that bounds it, can’t be visualized except in cross-sections—or, it is said, by a very few mathematicians like William Thurston of Cornell University—and can only be defined rigorously and elaborated upon by means of logical rules informed by a flickering intuition.
As with any important mathematical conjecture, there are partial results along the path to proving it on which later mathematicians must stand, as with Newton’s statement “we stand on the shoulders of giants.” In the case of the Poincaré Conjecture, partial results accumulated over time. In particular, these included proofs of the equivalent conjecture for spheres of dimensions greater than three, but not for three. Many brilliant mathematicians, among them Michael Freedman, Stephen Smale, John Stallings, and Christopher Zeeman, engaged in this work.
William Thurston and Richard Hamilton, a mathematician at Berkeley, made seminal contributions that pointed the way to Perelman’s proving of the much more intractable three- dimensional Poincaré Conjecture. Thurston speculated that there were only a small number of different geometries possible for three-dimensional shapes, from which the Poincaré Conjecture would follow as a corollary, but he didn’t prove it. Still, the suggestion and a partial proof of it stimulated more work on the Poincaré Conjecture by Hamilton and had a part in Perelman’s work as well.
Hamilton’s strategy, roughly described, made use of the fact that spheres of every dimension have a constant curvature. Therefore, if an undifferentiated blob in a higher-dimensional space could be kneaded and massaged and distorted, without puncturing or tearing, into something with constant curvature, then this would prove that the blob was, topologically, a three-dimensional sphere after all. To approach this constant curvature Hamilton used a mathematical tool called the Ricci flow. This is a mathematical method of transforming shapes that has somewhat the same effect as heat flowing through a space: as the heat flows it makes the temperature more uniform and in the process smooths out bumps and mountains, hollows and valleys, thereby revealing the underlying shape. Think of blowing hot air into a crinkled-up balloon.
Sometimes, however, it turns out that the Ricci flow must be interrupted at “singularities” (places where the process breaks down and part of the shape starts to stretch on and on, beyond bound—a little like dividing by zero) and a repair must be made using a controlled process of grafting on pieces of other shapes that topologists call “surgery.” Before Perelman’s work there was no guarantee that repairs could be made for every type of singularity and for every recurrence of the same type. Perelman dazzlingly showed that all possible singularities were reparable, and he demonstrated how to do the requisite surgeries and put all the stringy and lumpy pieces of the blob together. As Gessen writes:
He succeeded because he used the unfathomable power of his mind to grasp the entire scope of possibilities: he was ultimately able to claim that he knew all that could happen…as the object reshaped itself.
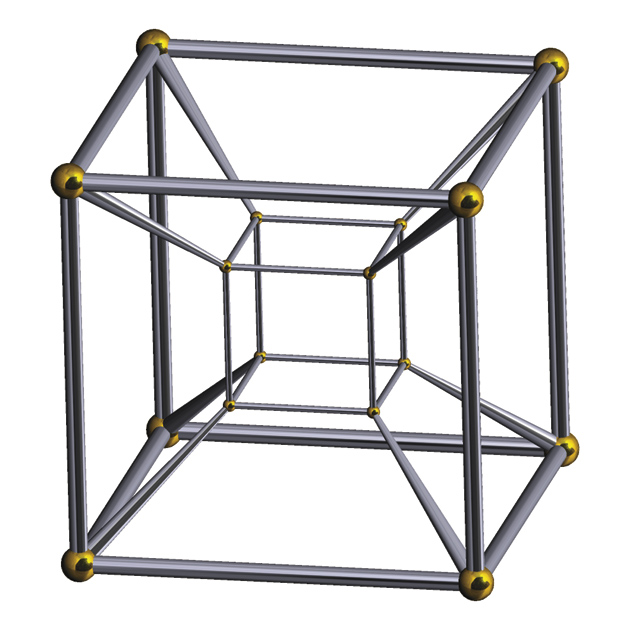
Robert Webb/Great Stella/Wikimedia Commons
A representation of a tesseract, the four-dimensional equivalent of a three-dimensional cube. It has sixteen corners and thirty-two edges to a cube’s eight and twelve.
Perelman’s three papers on the Internet outlining his proof set off a flurry of checking, explicating, and polishing among at least three sets of eminent mathematicians: Bruce Kleiner and John Lott, both of the University of Michigan; John Morgan of Columbia University and Gang Tian of MIT; and XiPing Zhu of Sun Yatsen University in China and HuaiDong Cao of Lehigh University. The checking was necessary because, as Lott wrote:
It has taken us some time to examine Perelman’s work. This is partly due to the originality of Perelman’s work and partly to the technical sophistication of his arguments. All indications are that his arguments are correct.
The vetting process also gave rise to the controversy brought to public attention by the New Yorker article “Manifold Destiny” by Sylvia Nasar, author of A Beautiful Mind , and David Gruber.2 A paper by Cao and Zhu had been originally entitled “A Complete Proof of the Poincaré and Geometrization Conjectures—Application of the HamiltonPerelman Theory of the Ricci Flow,” but after criticism, they revised it with the more modest title “HamiltonPerelman’s Proof of the Poincaré Conjecture and the Geometrization Conjecture.” They also toned down their original claim, “we give a complete proof,” replacing it with “we give a detailed exposition of the complete proof.” The original paper, which the eminent Harvard mathematician and Fields Medal winner ShingTung Yau initially promoted (Cao and Zhu were his students), seemed to some to arrogate credit for the final proof of the Poincaré Conjecture to themselves when what they were really doing was explicating and polishing Perelman’s work.
In 2006, Perelman turned down the prestigious Fields Medal, sometimes described as the Nobel Prize of mathematics, for his work in proving the Poincaré Conjecture. He explained, “Everybody understood that if the proof is correct then no other recognition is needed.” Whether because of the credit controversy, a disinclination to be in the public eye, or a generalized feeling of disgust, Perelman seems to have dropped out of the mathematical world, and he now lives with his mother in an apartment in St. Petersburg.
Up until March of this year, there remained one more chapter to the Perelman saga. Would he accept the one-million-dollar prize promised by the Clay Mathematics Institute for solving one of the seven so-called Millennium Problems? While the rules say that a proof must appear in a peer-reviewed mathematics journal (not just in an Internet posting), the mathematicians mentioned above have published papers in such journals expounding and amplifying the proof. Surely Perelman deserves the prize, which he was finally and officially offered on March 18.
Five days later, on March 23, Perelman rejected the Clay prize. He reportedly said through the closed door to his spartan apartment, “I have all I want.” The comments he made after rejecting the Fields Medal probably reflect his present state of mind as well:
I don’t want to be on display like an animal in a zoo. I’m not a hero of mathematics. I’m not even that successful. That is why I don’t want to have everybody looking at me.
Some might argue that monetary awards for mathematical work are inappropriate, or that the Poincaré Conjecture is of little practical value and not worth the one-million-dollar prize. The aesthetic and epistemic value of the proof is priceless, however, and it may eventually yield more earthly consequences as well. As for the size of the award—how many no-name hacks are there on Wall Street who make a million dollars or more not just once but every year, and contribute exactly what? Whether Perelman has practical need for the money or not, he could use it to help support his mother or mathematicians of his liking, or to advance the kind of education conceived by Andrei Kolmogorov, or for some purpose only he could imagine. Reconsider your decision, Grisha.
This Issue
April 29, 2010
-
1
Sylvia Nasar, A Beautiful Mind (Simon and Schuster, 1998), reviewed in these pages by Joan Didion, April 23, 1998; Graham Farmelo, The Strangest Man (Basic Books, 2009), reviewed in these pages by Freeman Dyson, February 25, 2010. ↩
-
2
August 28, 2006. ↩




