Prove It!

Mathematics is writing. For all the quantification it makes possible and all the technological and scientific discoveries it has helped to produce, it is ultimately words upon words. There is a bedrock of definitions (“A point is that which has no part,” says Euclid) crosscut by axioms (“A straight line segment can be drawn joining any two points”), whose only restrictions are that they not contradict one another. From this starting material we derive the terse assertions of consequences that are known as theorems and lemmas and corollaries. Were a theorem the result of a prosecutor’s successful argument, then the lemmas would be the settled issues of fact, the corollary the sentencing. The arguments are the key. These are the “proofs”—sometimes called “demonstrations”—without which the assertions are just so much blather. The proofs actually conjure mathematics into existence.

Stephen King has described writing as an act of telepathy across time and space.¹ This is surely true of mathematical writing: I’ve figured out that the square root of two is irrational—and this is my proof. What follows is as close to the written transmission of one person’s pure thought as any writing can be. But even in mathematical writing, it’s not just what you say but how you say it—better known as style.

This is the subject of Philip Ording’s 99 Variations on a Proof, which surveys different styles that can be used to prove a single theorem—a mathematical version of musical variations on a theme. In fact, there are one hundred numbered entries, beginning—according to the mathematician’s style—with chapter 0, a little math joke in itself. The entries range from the technical to the whimsical, from real proofs to more meditative reflections on the process and activity of mathematical research. But Ording’s book is more than just a survey. Each proof is accompanied by a brief commentary, outlining the inspiration of the variation and reflecting on the culture of mathematics through the ages. The less mathematically inclined reader might benefit from reading these commentaries first.

If one has any familiarity with mathematical proofs, it probably comes from a year-long sojourn into Euclidean geometry in middle or high school. For many, this is a jarring scholastic experience sandwiched between two years of algebra. Until that moment mathematics has been about finding the answer to a question: for example, “Sally rows downstream for 20 miles with a current of 2 miles per hour and the trip upstream takes 5 hours. How fast does Sally row?” In geometry, however, you’re told the answer—“If in a triangle two angles equal each other, then the sides opposite the equal angles also equal each other”—and then asked to find a reason, and explain it. QED.

Students learn in geometry that a mathematical proof has three simple ingredients: definitions, axioms, and deductions. The ways in which they logically combine—the recipe—depends on what you are cooking up. Definitions and axioms are statements whose truths are both obvious and incontrovertible (as in the example above involving the connection of any two points with a straight line), while deductions are statements that follow from the definitions and axioms, or even previously proven facts (which are themselves deductions), arrived at through the step-by-step application of deductive logic. Proofs are usually expressed in two columns, a sort of logical accounting ledger with assertions on the left and justifications on the right.

Such classical proofs read a little like a distillation of the Socratic method (“Well surely if you grant me that, then you must grant me this!”), and they can sound a bit like a prosecutor leading a witness to the nub of revelation. Many may be surprised to know that mathematical proofs often are text-heavy, even if symbol-laden, which is itself a form of stylistic evolution. In Carl Boyer’s timeless A History of Mathematics² we learn that in early Egyptian mathematics the unknown was referred to as “aha” for a “heap” of to-be-determined size—the sound of discovery and what was waiting to be discovered were one and the same. The letter x has been around as a symbol for millennia, including to mark the unknown on treasure maps, but it wasn’t until the seventeenth century that it began to represent the unknown in mathematical compositions.

A mathematical assertion often can be proved by many different kinds of arguments. Each proof should be correct and clear, and perhaps even captivating or charming. The way it is written may appeal to one kind of intellect or another (or sometimes none at all). But the style of the argument—the writing—is not just about convincing the reader; it is also about the manner in which the reader is convinced. One truth, but in the range of tellings, different aspects, implications, inspirations, and connections are revealed—just like great literature, but with “How do I love thee? Let me count the ways” traded for “How do I count these? Let me show you the ways I love best.”

Philip Ording is a professor of mathematics at Sarah Lawrence College. His interests include geometry and topology (especially the mathematics of knots), as well as the intersections of mathematics and the humanities. The organization of the book pays homage to its inspiration: the French polymath Raymond Queneau’s Exercises in Style (1947), which was itself inspired by Bach’s The Art of Fugue. Queneau’s book, Ording explains,

takes the same simple story—that of a peculiar individual who is first seen in a dispute on a bus, and then later in conversation with a friend about the position of a coat button—and transforms it in ninety-nine different ways.

Queneau was one of the founders of Oulipo, an avant-garde literary collective whose members included writers and artists ranging from Italo Calvino to Marcel Duchamp, as well as the mathematician Claude Berge, a pioneer in graph theory—a mathematical theory of connectivity that has found direct application in the broad and burgeoning study of networks, and even in formal literary constructions. “Oulipo” is short for “Ouvroir de littérature potentielle,” which translates to “workshop of potential literature.” It’s an appropriate name for a group that together investigated what literature could be rather than what it was, fueled by experimentation in literary production, often involving formal or rule-based systems.

Some connect Oulipo’s birth to Bourbaki, a collective of French mathematicians also united by a shared belief in the importance of formalism who strove to rebuild all of mathematics from the ground up, axioms first. Queneau is known to have attended at least one of their meetings, and the manifestos of Oulipo co-founder François Le Lionnais directly refer to the highly abstract elements on which Bourbaki was founded. Ironically, what was an avant-garde approach to literature was seen by many as reactionary when it came to mathematics.³ Bourbaki’s stripped-down axiomatic framing waxed briefly and has since waned.

Queneau didn’t just admire mathematics. He published two peer-reviewed papers, both on “s-sequences”: lists of numbers characterized by conditions such that any number in the list depends in certain ways on numbers that precede it.⁴ You don’t need to squint to see this as an abstraction of writing. In one of Queneau’s last works, Les fondements de la littérature d’après David Hilbert, he pushes the analogy, turning the axioms of geometry (as written by the mathematician David Hilbert, a towering figure and great fan of formalism) into axioms for literature. Points become words, lines become sentences, and planes (infinite flat sheets comprising lines and points) become paragraphs.

Each of Queneau’s ninety-nine variations in Exercises in Style demonstrates that even the simplest set of facts can be brought differently to life by a range of storytelling styles. In this way it is something like a literary version of Euclid’s Elements, whose many more mathematical “stories” derive from five (or ten, depending on how you count) simple axioms, each even plainer than the few quotidian activities that define Queneau’s peevish hero.

The variations in Queneau’s Exercises in Style include a sonnet, a book blurb, and a one-act opera. There is a musical score. An entry titled “Zoological” is animated with animals (“In the dog days while I was in a bird cage…”). And of course there is mathematics. “Negativities” is the story of what it is not (“It was neither a boat, nor an aeroplane…”). “Probabilist” works in the theme of chance. First reading aloud and then disentangling the mathematically sophisticated “Permutations by Groups of 2, 3, 4 and 5 Letters” (“Ed on to ay rd wa…” becomes “One day toward…”) is a delight, even if you have to work a little. As a whole, Queneau said in a published conversation with the French painter and poet Georges Ribemont-Dessaignes, he hoped that the collection might act as a “rust remover of literature” without “boring the reader too much.”

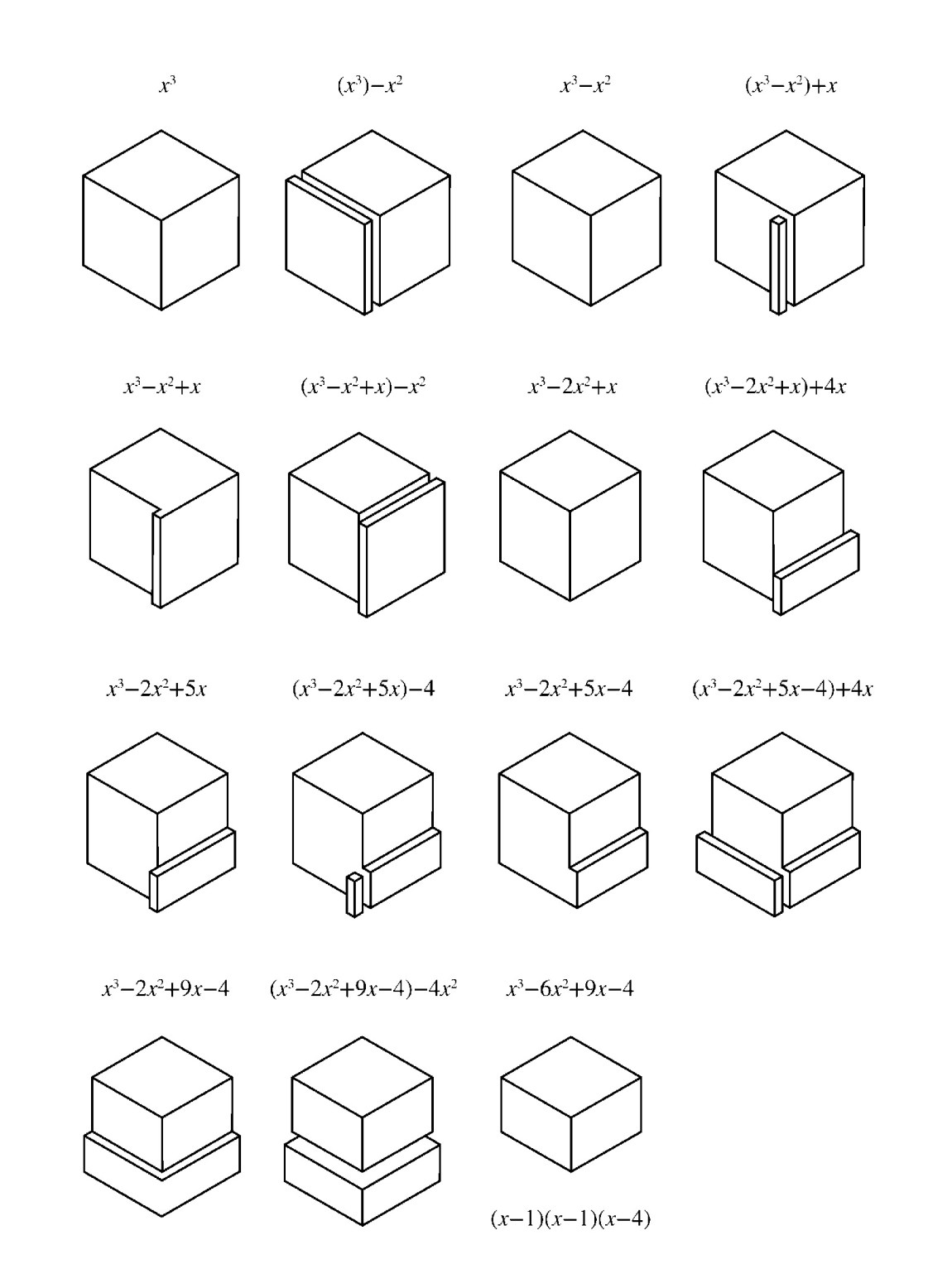
In 99 Variations on a Proof Ording explains that, after discovering Queneau’s Exercises in Style, he “wanted to see what effect constrained writing strategies would have on a mathematical narrative—a proof.” Mirroring Queneau, each of Ording’s variations is born of a simple fact, but a mathematical one, expressed in this cubic equation:

Let x be real. If x³–6x²+11x–6=2x–2, then x=1 or x=4.

Admittedly, there is a bit to unpack here. For starters, this equation involving interacting cubes, squares, and the like is just an example of “solving for x,” where you discover that if you plug in 4 for x on both sides you get the same number (6), and if you plug in 1 for x on both sides you also get the same number (this time it is 0).⁵ But—and more interesting—these are the only two “real” numbers (i.e., numbers with decimal expansions or numbers on the familiar “number line”) for which this is true. This part of the proof reaches back to the earliest recorded arithmetic exercises, in which a “proof” was an actual demonstration of a calculation.

Ording’s choice of theorem runs the risk of being a deterrent to readers with “little or no predisposition to the subject matter,” whom he hopes to attract. It introduces a heavy dependence on notation—x’s and y’s make regular appearances among the hundred variations—and there is a fair amount of moving them about through the use of algebra. Legend has it that Stephen Hawking’s editor on A Brief History of Time warned him that every equation included in the book would reduce his audience by half. He chose to include just one: E=mc². By that arithmetic, this little aside and the paragraph above may have cost us fifteen sixteenths of our readers. Ording’s book would suffer an even more dramatic loss.

But Ording’s assertion seems a clear nod to Queneau. As a simple (even “boring”) statement that two combinations of numbers work out to be the same, it serves as a mathematical doppelgänger for Queneau’s bumptious commuter. That it too could inspire so many variations and accompanying reflections deserves applause, even from the non-predisposed reader.⁶ There is much that can be learned—and plenty of rust to be removed—for both the uninitiated (but open-minded) and the sophisticated.

Early mathematical arguments and styles are well represented in the book, ranging from an imagined Babylonian justification (chapter 16, “Ancient”) to a proof using Euclidean geometry (chapter 52, “Antiquity”). I’d challenge anyone to check the work in the glyphs that make up the former. Chapter 88, “Dialogue,” is a back-and-forth between a master and a disciple—a form of reasoning through a problem that Ording posits is “a likely candidate for the oldest style of presenting a mathematical argument.” Some variation of it still goes on during office hours all around the world.

There are two medieval efforts, each of which serves as an example for the utility of a simplified—even if abstract—notation that cleans up the flowery and somewhat laborious text. English is really not well suited to algebra. The first, chapter 34, is formatted to look like an illuminated manuscript and restates the theorem as follows:

Suppose that the intensity of a quality is as the cube of its extension and 9 times that less 6 times its square. It will be demonstrated that when this quality achieves an intensity of 4, its extension is 1 or 4.

In the accompanying commentary Ording credits the proof as following the method of Leonardo of Pisa (aka Fibonacci) and the scholastic philosopher Nicole Oresme, with connections to an ancient Chinese text, The Nine Chapters on the Mathematical Art.

The second medieval-style proof, chapter 70, continues the high language but in a normal font, opening with “In the name of God, gracious and merciful!” and closing with “It is now time that we should conclude this demonstration with gratitude to God and praising all of His prophets.” Sandwiched between is a clever geometric proof that includes circles, conics, and intersecting lines. We learn from Ording’s commentary that this kind of proof could be found in the eleventh-century Treatise on Demonstration of Problems of Algebra, a masterpiece by the Persian mathematician Omar Khayyam, who is now surely better known for his poems in the Rubaiyat.

Khayyam’s Algebra was the first written attempt to address all the ways in which cubic equations can arise and then be solved via clever geometric constructions. With no x’s and y’s present it may seem to the modern reader to be ironically titled, but the word “algebra” is derived from the Arabic al-jabr, which refers to the process of simplification (e.g., “cancellation”) of mathematical relations. Its origin is usually attributed to the ninth-century Persian mathematician al-Khwarizmi, whose name lives on in the word “algorithm,” which refers to any recipe of instructions that underlies a computer program and, for some, is poetry of a different sort.

Fast forward several hundred years to Renaissance Italy, where solving equations was a form of dueling, with mathematicians challenging one another to contests for money and honor. Ording memorializes this in chapter 43, “Screenplay,” a script in which a character announces:

I hereby declare that on this the tenth of August in the year fifteen hundred and forty-eight of our Lord in our fair city of Milan, the visitor Niccolò Fontana Tartaglia of Brescia challenges Girolamo Cardano, represented here by Ludovico Ferrari Esquire, to a duel of the mind. The dishonored shall pay the winner two hundred scudi.

All of the characters mentioned here are real historical figures. Out of such challenges grew formulaic approaches to the solution of the cubic equation you get if you move the pieces around in Ording’s original theorem.

Such a formula—analogous to the famous quadratic formula—is among the discoveries to be found in Ars Magna, Girolamo Cardano’s sixteenth-century magnum opus. Elsewhere Ording reproduces a two-page spread from Ars Magna (chapter 7, “Found”) with the exact cubic relation that is the focus of the book. Ording claims to have been “stunned” to find it there, but one can’t help but wonder if that isn’t where his project started. (There are an infinite number of cubic equations with real solutions to investigate.) References to Cardano are sprinkled throughout, suggesting that he’s something of a hero to Ording. Khayyam also receives a handful of mentions, but generally—as Ording points out in chapter 71, “Blog”—early Eastern contributions to mathematics continue to be less well known to Westerners than their later Western counterparts.

The order of the variations in Ording’s book confuses the timeline of discovery, even if it might reflect the timelessness of mathematical truths. But 99 Variations on a Proof is not really meant to be a history lesson, even if it is by necessity partly that. One aim is to display the variety of possible proofs, the different ways in which we might convince one another that there are only two solutions, 1 and 4, to this little problem. To this end, various proofs exhibit particular styles of logical argumentation, including at least two that involve indirect argument.

Chapter 13, “Reductio ad Absurdum,” bears the title of a form of proof in which one assumes the conclusion to be false—that there is another solution different from 1 and 4—and with that additional hypothesis, as Ording explains, concludes that “some third statement that was already known to be true—an axiom or proven proposition—is false,” in this case that 0=1. This is a roundabout way to show that the stated conclusion must therefore be true—a feat of logical magic called a “proof by contradiction” that makes use of the famous “law of the excluded middle”: either there is a third solution or there isn’t, and no other option (“the middle”) is available. Here Ording quotes the Hungarian mathematician Georg Pólya, who noted that this kind of indirect proof “has some resemblance to irony which is the favorite procedure of the satirist.”

Similarly, chapter 14, “Contrapositive”—which also relies on indirect argument—makes use of the fact that proving an “If this, then that” statement is equivalent to proving “If not that, then not this.” These introductions to the mechanics of logic are for me like little mathematical madeleines. I recall my own early difficulties with the language of mathematical proofs. It took me several weeks in my first pure math class to understand that the technical meaning of “A if and only if B” is both that A implies B and that B implies A, and not just that the author was being emphatic about B following from A.

There are also several proofs here—chapter 0, “Omitted”; chapter 44, “Omitted with Condescension”; and chapter 94, “Authority”—that aren’t really proofs at all: each in its own way says “this is obvious” and doesn’t actually do the work of demonstrating anything. Ording uses “Omitted” to talk about the idea that choosing to prove something is part of the “aesthetic” of writing mathematics or about mathematics. He uses the other two chapters to call out some of the ways in which pedagogy can be lazy or even cruel. “Authority” produces a proof that says only that “it follows from Euler,” one of the great mathematicians of all time, whose collected works fill ninety volumes. Good luck finding that reference. I can’t count the hours of self-flagellation I’ve experienced laboring (and swearing) over the word “obvious” in a textbook or research paper. These madeleines are migraines. As Ording says in the commentary accompanying “Authority,” “When the authority of reference is oneself, a proof by authority becomes a proof by intimidation.”

As the saying goes, sometimes words are not enough, even in mathematics. Mathematical inspiration and argumentation often make use of the visual—which for some mathematicians might not rise to the level of a proof, but could very well be more convincing for those who blanch at symbols. These make for some beautiful variations. A favorite is chapter 10, “Wordless,” a visual proof—or “Proof Without Words”—based on Ording’s Euclidean chapter 52, “Antiquity.”⁷ It uses drawings of cubes, squares, rectangles, columns, and lines, and makes tangible the manipulations of algebra that to many can seem inscrutable. This is also called a “Look-see! Proof.”

A paper-folding diagram in chapter 39, “Origami,” shows that abstract arguments can be made physical, and the photograph that is chapter 29, “Model,” shows a delicate and beautiful paper-model embodiment of a solution. As one who has always had trouble “seeing” mathematics, I found these pictorial arguments a delight.

Some mathematical styles have to do with genre. An algebraic style of argument—such as chapters 23 and 24, “Symmetry” and “Another Symmetry”—will almost surely include a lot of formula rewriting and make use of symmetries, sometimes symbolic (“cancel out the x’s”), but other times reflected in a pictorial or geometric representation. “If a problem will divide along a line or axis of symmetry,” Ording notes, “it means there’s a good chance that a solution to one part of the problem will extend…to the problem as a whole.” A geometric proof will frame the assertion using the familiar lines, curves, and notions of distance in a two-dimensional or three-dimensional space, or if necessary might even require analogous “objects” that reside in spaces of higher dimensions or having exotic curved or crenellated structures.

Topological arguments—as in chapter 51—can have a geometric feel but allow the freedom to slide, squash, and squeeze the shapes. An analytic proof, such as chapter 33, “Calculus,” will usually involve techniques that derive from or are related to calculus. On the whole, it is not uncommon in mathematics to use newly developed ideas and subject areas to reprove old and seemingly settled problems; as with many kinds of writing, old themes revisited in new styles have the power to reveal previously unseen subtleties or even produce simpler arguments than the original.

Some of Ording’s variations give readers a glimpse of the culture of mathematics as a practice. Chapter 48, “Computer Assisted,” shows how computers are now used not just to solve equations but to assist with or even fully produce proofs. Doron Zeilberger, a mathematician at Rutgers, has even listed his computer program “Shalosh B. Echad” (a Hebrew-English mashup based on the model name of Zeilberger’s first computer) as a coauthor on some of his published papers. More recently, the same technologies that are producing machine-written news articles are also being used to solve math problems.

In a different direction, computers can now provide the modern mathematician with a platform for experimentation, giving mathematics more of the laboratory feel of the physical or life sciences. For many this has changed the way mathematics is approached—see, for example, chapter 76, “Experimental,” and chapter 77, “Monte Carlo”—as well as the way in which mathematics is written. The latter is the source of another variation, chapter 35, “Typeset,” which gives a window into the TeX typesetting software package (invented by Donald Knuth, a computer scientist at Stanford) that has revolutionized the production of mathematics papers and the pace of modern mathematical research.

This acceleration in the production of new mathematical ideas is transformative for the discipline. Historically, mathematics has been among the slowest of the sciences. Articles submitted for peer review can take years before they are returned with comments that may then need to be addressed and the articles returned for second reviews before acceptance for publication—if accepted at all. But nowadays mathematicians often deposit preliminary versions of their papers, known as “preprints,” on arXiv.org, a digital depository and preprint server, which accelerates the availability of the work at the expense of detailed review; Ording refers to this in chapter 37. Some mathematicians—most likely those with tenure—may not even go to the trouble of pursuing official publication.

Despite all the new ways of doing mathematical research, most mathematicians are still attached to the chalkboard—a picture of which is shown in chapter 21, displaying Cardano’s method for finding the solutions to the book’s ur-equation. “More than a teaching aid, a blackboard is a medium for mathematics,” Ording writes, although it can also be “a source of anxiety” for a student “when called to the board.” But that’s often where the hard work is done: scribbling, erasing, working out examples in front of colleagues, even sketching cartoons as inspiration. Around 3,500 years ago in Mesopotamia traders scratched marks on clay to work out the proto-problems of mathematics. In that sense, little has changed. For further evidence, I recommend Jessica Wynne’s Do Not Erase: Mathematicians and Their Chalkboards,⁸ a collection of photographs of the chalkboards of mathematicians from around the world, each accompanied by a reflection or explanation from its creator.

The chalkboard is just one meeting place for ideas. Ording points out that “many university mathematics departments hold tea in the afternoon,” creating “a venue for informal discussion.” Ours at Dartmouth is every weekday, usually at 3:30—come visit. Chapter 65, “Tea,” is an imagined exchange during such a get-together. The participants include a person referred to as Lambda, who has just proved Ording’s theorem by complicated means—see chapter 64, “Research Seminar”—and a few attendees, buttonholing (à la Queneau?) Lambda for details or maybe just to strut their stuff. Ording cleverly has tea follow a seminar, as is often the case in real life.

Group proof efforts of course no longer require contributors to be in the same room. Chapter 25, “Open Collaborative,” is an imagined exchange on a blog thread, and those interested in this lively online research culture might make an excursion to the Mathematics Stack Exchange website; it’s not just students hunting for homework solutions. An updated version of Ording’s book might have to add an entry: chapter 100, “Zoom.”

This is of course but a sampling of Ording’s mathematical buffet. The more linguistically inspired variations in the book feel like direct tributes to Exercises in Style. Chapter 9, “Monosyllabic,” is a proof using words of only one syllable. Chapter 81, “Doggerel,” is written in verse and resembles, Ording notes, a “stanza from Lewis Carroll’s double acrostic, The First Riddle.” Chapter 98, “Mondegreen,” is—as per the definition of the word—a homophonic rewriting of the proposition:

Their omelette: eggs, beer, eel.
If eggs cued my nose, six eggs queered.
Plus nine eggs.
My nose for equals—zero.
Then, egg sequels one or four….

“Whenever I see the ubiquitous rubric ‘Theorem. Let…,’” Ording explains, “I cannot help but hear ‘their omelette.’” These proofs’ playfulness at the boundary of sense and nonsense surely expands the limits of mathematical exposition as well as readerly response to mathematical ideas. I think Queneau would have been proud.