Nature, and Nature’s Laws lay hid in Night.
God said, Let Newton be! and All was Light.
It did not last: the Devil howling “Ho!
Let Einstein be!” restored the status quo.
—J.C. Squire, “In continuation of Pope on Newton”
 The year 2016 is either the hundredth or the hundred and first anniversary of Einstein’s general theory of relativity and gravitation. He had given versions of it, some incorrect, which were published in brief communications in the Prussian Academy of Science proceedings in 1915, before finally finding the correct one on November 25 of that year. The correct theory was masterly summarized in 1916 in his Annalen der Physik paper, which many people refer to as its definitive formulation. The journal received the paper on March 20, 1916. One of the reasons for the almost frantic pace at which he sought to present his theory to the public was that he thought that the great German mathematician David Hilbert might beat him to it. It turned out that Hilbert never really had the right theory.
The year 2016 is either the hundredth or the hundred and first anniversary of Einstein’s general theory of relativity and gravitation. He had given versions of it, some incorrect, which were published in brief communications in the Prussian Academy of Science proceedings in 1915, before finally finding the correct one on November 25 of that year. The correct theory was masterly summarized in 1916 in his Annalen der Physik paper, which many people refer to as its definitive formulation. The journal received the paper on March 20, 1916. One of the reasons for the almost frantic pace at which he sought to present his theory to the public was that he thought that the great German mathematician David Hilbert might beat him to it. It turned out that Hilbert never really had the right theory.Most theories in physics are produced in response to some experimental phenomena. The quantum theory is like that: the phenomena seemed so weird that they cried out for a new theory to explain them. While there were some anomalies in the planetary orbits that needed explanation—at one point it was even suggested that an unobserved planet might be responsible—this is not what motivated Einstein. He was trying to fit gravitation into the worldview he had created with his 1905 special theory of relativity. It took him a decade to do this and he had to learn some mathematics that had never been applied to physics. A mathematician named Marcel Grossmann whom Einstein had known since his student days in Zurich helped him.
Here is the theory:
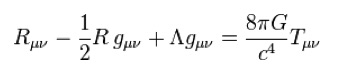
The term with the capital lambda is the cosmological constant. The term on the right hand side multiplied by Newton’s gravitational constant G is the matter term. The other two terms contain the geometry of curved space.
The key to the whole business turned out to be what it means to be “weightless.” Suppose someone is standing on a scale that gives way so he or she falls freely. What will the scale read? The answer is zero. As far as that person is concerned the effect of gravity has disappeared. When later Einstein tried to explain this to lay people he introduced the metaphor of what became known as the Einstein elevator. He imagined an elevator somewhere in outer space, far from any gravitating object. He imagined a genie that could pull the elevator up by a rope so that it had any acceleration one wanted. If he pulled it up with exactly the acceleration of a freely falling body on Earth then the occupants of the elevator would think that they are in the Earth’s gravitational field. One can thus switch on and off the effects of gravity by changing the acceleration. This is known as the “principle of equivalence.” It has remarkable consequences, as Einstein discovered. One of them that I will now explain is that space in the presence of gravity is “curved.”
Light in a vacuum propagates in straight lines. If you made a triangle of three light beams you would find that the interior angles add up to 180 degrees—as Euclid said. This is the “flat” space prediction. Now let us return to our elevator. With the elevator stationary, we emit a light beam from one side and it propagates to the other in a straight line. It is always the same distance from the floor. Now we do the same thing when the genie pulls up the elevator. The floor keeps rising to meet the light beam, so viewed from inside the elevator the beam follows a curved path toward the floor. If we make a triangle of three of these curved light beams the angle sum will no longer be one hundred eighty degrees but might be greater or lesser. Space has become curved and the geometry is no longer Euclidean.
But by the principle of equivalence this setup can be replaced by a stationary elevator in a gravitational field. Gravity curves space. Light follows the straight lines in this space as do other gravitating objects. In relativity, space and time must be treated together so it is more correct to say that the geometry of space-time is curved. The difficult mathematics is going from a distribution of matter to the geometry of space-time. Now there are computer programs that do this for you, at least in some cases. Einstein was able to study simpler cases where at least he could do this approximately.
This explains the anomaly in the orbit of the planet Mercury. Mercury is following the curved path that is determined by the geometry of space-time created by gravity. In Einstein’s theory of gravity there are no gravitational forces, only the curving of space-time. Einstein proposed that this could be tested by observing the bending of starlight by the gravitational field of the sun. This was tested in the 1919 expeditions led by the British astronomer Sir Arthur Eddington to observe stars during a total eclipse of the sun. The results, which showed, as predicted, an observable displacement of the star’s observed position due to the gravitational bending of light, agreed with the theory and Einstein immediately became a world celebrity.
After 1915 he continued drawing out consequences of the theory. One of them was the notion of a gravitational wave. An accelerating gravitational object can emit waves of gravity, but these waves show up as distortions in space-time. Einstein proposed this in 1916 and it has been detected indirectly by observing the orbits of neutron star pairs. Very elaborate experiments are now underway to detect them directly. Einstein also noted that a star could act like a gravitational lens and distort the image of a star behind it. He thought that this effect would never be detected but it is now a commonplace tool of astronomers.
Advertisement
In 1917 Einstein published a paper on the application of the theory of relativity to the universe at large—cosmology. He had decided that the universe was stationary—neither expanding nor contracting—so he added a term, the cosmological constant, to his original equations with a value of the constant, the Λ in the above equation, chosen to guarantee this. He abandoned this once it was shown in the 1920s by Edwin Hubble that the universe was actually expanding. Now it has been shown that the universe is expanding at an accelerating rate—so the cosmological term is given a new value, the dark energy, now adjusted to produce the acceleration. This is typical of what has happened in the last few decades. Cosmology, aided by some marvelous experimental discoveries, has become the center of attention. There is nothing more exciting.
Among the cosmological phenomena that the theory of relativity successfully predicted was one that Einstein could never accept: the existence of black holes. In fact, in 1939 he wrote a paper arguing that what we now call black holes violated his theory of relativity. He submitted the paper to the Physical Review. It was sent to a referee who rejected it, so Einstein then published it in a mathematics journal, Annals of Mathematics. The math of his paper is correct but irrelevant, since what he showed was that to form a black hole one needs stellar collapse.
Einstein was apparently unaware that around this time Robert Oppenheimer and his students had shown that if a star was massive enough it could collapse into a black hole. After the war, Oppenheimer decided that this was of such little interest that he refused to discuss it. He did not live long enough to learn about the work of Stephen Hawking, who showed that black holes can actually radiate and eventually disappear. Today, there are, as far as we know, massive black holes in the center of every galaxy, including our own.
It was probably the work of Hawking, and of course the astronomical discoveries, that revived interest in black holes. I have a vivid memory of a small meeting I attended at the Institute for Advanced Study in the late 1960s, after Oppenheimer’s death. Indeed, the meeting was in his honor. There was an extraordinary array of physicists on hand including people like Murray Gell-Mann and Richard Feynman, my teacher Julian Schwinger, T.D. Lee, and C.N. Yang—Nobelists all. The talks were about the latest theories and experiments. John Wheeler wanted to give a talk on black holes. There was so little interest that his was the last talk on the last day, and some people had already left.
Wheeler spoke about a theorem that he called the “no hair theorem.” This is the statement, still not proven in general, that, viewed from the outside, black holes exhibit only three properties—their mass, their electric charge, and, if they are rotating, their angular momentum. What they are made of is irrelevant. This is now a basic element of the theory of black holes, but as Wheeler was describing it, no one was paying the slightest attention, with the exception of Freeman Dyson, who understood its importance. That is the only thing I remember from that meeting, but Dyson was right.
I often think of the exchange Einstein had in 1919 when a cable came to him in Germany from Eddington informing him that his general theory of relativity and gravity had been confirmed. A student was present and she asked how he would have felt if it hadn’t been. He replied “Da kömmt mir halt der liebe Gott leid tun, die Theorie stimmt doch.” “I would have been sorry for the dear Lord—the theory is correct.”
I do not think he ever changed his mind about black holes.


